『高校物理の勉強法は?』
『高校物理の成績アップのコツは?』
『物理が苦手なのはどうすれば解決できる?』
と悩むこともありますよね。
中学までは理科という1つの科目だったものが、高校に入り、より専門的になっていきます。
その一つが、物理基礎と高校物理です。
「物理って才能ないと無理なんでしょ」
「物理、難しくて……」
そのように思っている方も多いと思います。
ところが、それは誤解です!
物理はコツをしってしまえば、点数が取りやすい科目になっています。
この記事では、物理の苦手を克服したい方やこれから物理を学ぼうとする方に向けて、物理の勉強法やコツを解説します。
この記事の筆者は、旧帝国大学にて物理学の博士号(Ph.D.)を取得した、とぷぶが担当いたしました。学習塾での講師もおこない、物理の苦手な生徒への指導経験も豊富です。物理を数式よりもイメージや言葉で理解することを大切にしており、多くの生徒の成績向上に貢献してきました。
この記事の目次
高校物理は簡単と考える!センス要らない

物理と聞くと言葉を聞いただけで「難しそう」と思い込んでしまう方がいます。
ただ、実際には、さほど難しいものではありません。
なぜなら、物理は、普段身の回りで起きていることを扱うからです。
例えば、小さい頃の滑り台、電車に乗っているときに力のかかり方、部活でキャッチボールをするときに力、など皆さんは普段から物理を学んでいるのです。
たまにしか学ばない英語の方がよっぽど難しいでしょう。
では、物理基礎、高校物理を学ぶ上で大切なことを解説していきます。
物理で必要な数学のレベルは?微分積分って必要?
物理というと、難しい数式がたくさんでてくるというイメージがあるのではないでしょうか?
実際、読み方さえ分からないような物理の数式がアニメやドラマに並んでいたりしますよね。
確かに、大学以降の物理は高度な数学が必要になりますが……高校物理ではそんなことないのです!
たくさんの文字が出てくるものの、数学自体のスキルは中学生レベルで十分なことが多いです。
プラスして三角関数(sin, cos)とベクトルが出てきますが、それでも基本的な使い方しかしません。高校で習う数学に比べると圧倒的に簡単。
ですので、「なんか数式が難しそう……」という理由で物理を避けているのだとしたら、もったいないことです。
中には、「でも、高校物理って本当は微分・積分が必要なんでしょ」と思っている方もおられるかもしれません。
微分・積分が必要だとなるとやっぱりちょっと数学的に難しくなってしまいます。
しかし! 大切なのはむしろ物理のイメージや意味であって、微積分ではありません。
それさえしっかりしていれば、高校物理の範囲はだいたい、なんとかなります。
高校物理で覚えるべき公式パターンはそんなに多くない
高校物理の教科書を見ていると、たくさんの公式が出てきますよね。
この辺りも「物理って難しそう」となる原因の一つかと思います。
等加速度直線運動のページだけを見ても、どっさりと式が……。
ところが、物理の問題はパターンがある程度、決まっているのです!
英語の文法や単語を覚えることを思えば、覚える量ははるかに少ないですし、数学の解法パターンに比べても、断然多くありません。
つまり、(後述のイメージをしっかり押さえたうえで)基本の問題を練習すれば、得点アップにつながります。
物理の苦手意識をなくす方法
嫌いなことや苦手意識を持っていることってなかなか、勉強がはかどりませんよね。
だけど、成績を上げたいから無理やり勉強しなきゃ、と頑張るわけですが、やっぱり効率は落ちてしまいます。同じ時間を使うなら効率よくやりたいですよね!
一番いいのは物理を好きになってしまうことですが、それができたら人間、苦労しません。
そこで、少しでも苦手意識を取る方法を考えてみましょう。
問題が解けないのは問題集が悪い
人間の感覚というのは意外といい加減ですし、変化していきます。今、苦手だと思っていたとしても、それは変えることができるのです。
そもそも、どうして苦手意識があるのでしょうか?
こう聞かれると、
「数式があるから」
「難しい言葉がたくさん出てくるから」
などなど多くの答えが返ってくると思います。しかし、それは嫌いな理由であって苦手な理由ではないはずです。苦手な理由はもっとシンプルで、
問題が解けない、点数がとれない
これに尽きるのではないでしょうか。
点数が取れないから苦手意識が生まれ、苦手意識が、勉強の効率を下げる、という悪循環。
それを断ち切るには、自分に合った参考書、問題集を選ぶ、これに尽きます。とにかく書店などで多くの問題集をぱらぱらっとめくってみましょう。
例えば、苦手な方向けには大塚 聖・著『高校とってもやさしい物理基礎』を読んでみてはいかがでしょうか。
独学でも読めるように配慮してあり、書き込み式なので、取り組みやすいです。
また、問題集ではありませんが、初歩のところから理解したい、イメージをつかみたい、という方には鯉沼 拓・著『宇宙一わかりやすい高校物理』シリーズをお勧めします。
まずは一番簡単そう、と思うものを選びます。
解ける問題を解いているうちに苦手意識が薄れていきますし、実際に実力も上昇していきます。
めちゃくちゃ単純な話ですが、人間の脳は意外にいい加減にできているものです。
自分は物理の問題が解ける、そういう体験を積み重ねましょう!
物理の基本・公式を覚える前にやること
物理の勉強と言うと、とにかく公式を覚えて…という方は多いのではないでしょうか。
そして、たくさんの公式にうんざりして嫌になる…、これがあるあるだと思います。
そういう勉強法はよく分からないが積み重なって辛いし、間違っているのです。
数式よりも大切なのは『言葉』の理解
実は、物理の公式を覚えるより先に、絶対にやらなければならないことがあります。
それが、言葉の意味をきちんと覚える、考える! です。
どういうことでしょうか? 具体的に見てみましょう。
例えば、よく見る公式
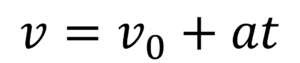
がありますよね。ここで大事なのは、この公式よりもvとはなにか? aとはなにか? という意識。
もちろん、vは速度、aは加速度、tは時間となっているのは教科書を見ればわかりますが、それより一歩踏み込んで理解してみます。
速度 : 単位時間あたりに進んだ長さ
加速度 : 単位時間あたりに変化した速度
うーん、なんだか小難しそうな言葉ですね。
しかし、ここでしっかりこの言葉をかみ砕いて行くことが大切です。
速度というのは、1秒間にどれだけ動けますか、ということで、それを難しく言うと上みたいになるんですね。
でも、その意味は繰り返しますが、1秒あったらどれだけ動くか、ということを言っているだけです。
加速度というのは、1秒間にどれだけ速度を増やせるか(マイナスの時は減らします)ということを言っています。
だから加速度が5 [m/s^2]だとすれば、1秒たてば速さが5 [m/s] 増えますし、3秒たてば5×3 = 15 [m/s] 増えるというわけです。
そう考えると公式でどうして a×t という部分があるのかわかりやすいのではないでしょうか。
等加速度直線運動についての詳しい話は後述します。
こうして、言葉の意味をしっかりさせてから公式を見ます。
そして、覚えるよりも、その公式を使う練習問題を何問か解いて、どういう使い方をするのか感覚をつかみましょう。
最初は答えを見ても構いません。
ちなみに、ここで出てきた単位時間、という言葉以外にも物理には単位○○、という表現が多いです。
1つのイメージとして、単位○○あたりと出てきたら、○○で割っている、というイメージ(正確には微分になりますが……)を持つと理解がはかどるかもしれません。
単位質量あたり、と言われてたら、ああ、これは質量で割るのかな、という感じですね。
絶対に図を描こう
次に、物理の問題を解くときに必須になるのが図を描くこと!
文章だけの問題を見ても、なかなかイメージがつかめません。
しかし、図にして、必要な数値などを書き込んでいくと、一気に脳内がクリアーになりますし、物理的なイメージがわきやすくなります。
図が描ければ、半分以上問題を解き終わっていると言ってもよいくらい大事なのです。
物理が苦手……という人の多くが図を描いていないように思います。
一つの理由は描き方がよく分からない、というのがあるでしょう。
そこで最初は、問題集などの解答にある図をノートにうつして練習します。
答え合わせの際、数式だけ書いて終わり、という勉強をしている方も多いでしょうが、必ず、図もセットで描くことをお勧めします。
特に、運動方程式を立てる、というとき、力がどうかかっているか、というのが分からないとできません。
斜面を転がる問題であれば、
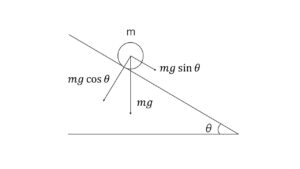
のような感じが一例でしょうか。
コツは
1. sin, cosを間違わないこと!
力や速度を縦、横に分けるのにたくさん出てきます。
ここを間違うと他がすべて合っていてもダメなので、きちんと練習です。
2. 力は基本的に、くっついているところに働く。
糸がくっついていれば、必ず糸から力がかかっていますし、床の上にあれば、床からの力があります。
例外として、重力、電磁気力は離れていても働きますので気を付けましょう。
物理は力学が基本
歴史的に見て、最初に誕生したのが力学でした。
ですので、力学がその後の物理の基礎となっています。
ここでは簡単に力学ってどんな感じでイメージをつかんでいけばよいのか、見ていきましょう。
等加速度直線運動の公式と大切なイメージ
等加速度直線運動の公式といえば、
式1.
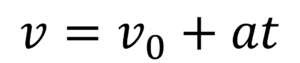
式2.
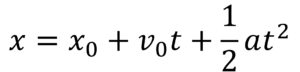
式3.

の3つが基本ですよね。ここでは、このうち、特に式1と式2について考えます。
式3は実は力学的エネルギー保存の法則のことなので、ここではなく、あとで見ましょう。
まず、等加速度ではなく、それより簡単な等速運動、つまり速さが変わらない運動で速さと距離のイメージを固めます。
小学校の授業を思い出すと、距離 = 速さ × 時間 でしたよね。
これをグラフで描いてみます。縦軸に速さ、横軸に時間をとると、

となります。
赤い線が一定の速さ v を、青い点線が時間 t を表しています。
こうして見ると一つの事実に気づきます(図のところでも述べましたが、人間は目で見ると、たくさんのことが理解できます)。
それは
緑色の面積 = 距離
です。
先ほどの距離の式を文字を使って表すと、距離 = v × t となりますよね。
このグラフで横は t 、縦は v の長方形になっていますから、確かに面積になっています。
実は、これは等加速度運動になっても変わらないんです!
それを手がかりにして、どうして式2が成り立つか考えてみましょう。
同じように、速さと時間のグラフを書きます。
ただし、今度は速さが時間によって変わります。具体的には式1のように。
これは一次関数の形になっていますね。切片が v0, 傾きが a の直線です。
※一次関数は y = a x + b というものです。
グラフの形がぱっと分かりにくい人は、y → v に、x → t に、 b → v0 に置き換えてみましょう。
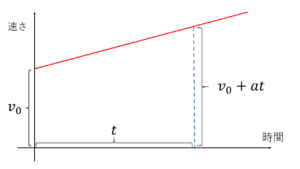
そのようなグラフを書いたのが上の図になります。
最初の速さが v0 で、時間が t だけたったときの速さは v0 + at です。
この面積が進んだ距離になるので、面積を計算してみましょう。
台形を横に倒した形なので、台形の面積の公式を使います。
台形の面積 = ( 上底 + 下底 ) × 高さ / 2
ですので、
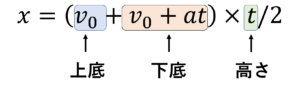
となりますね。これを計算すると、
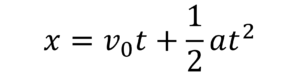
となり、式2が出てきました。
あれ、式2と比べて、x0 がないぞ、と疑問に思われた方もいるかもしれませんが、これは大した問題ではありません。
x0 = 0 とすれば、同じになりますから。
このように、速さ-時間のグラフの面積が距離になるというイメージを大切にしましょう。
また、このグラフでの傾きが加速度 a である、というのも忘れずに。
力と運動方程式
運動方程式は物理の主役とも言える存在です。
運動方程式自体は、式で書くと
ma = F
というシンプルな形をしています。
m は質量 [kg], a は加速度 [m/s^2], F は力 [N] です。
イメージ的には、重いものほど動かすのは大変だ、という法則になります。
加速度を 5 欲しいとして、質量が 10 の時と、100の時を考えます。
質量 m が 10 の時は、F = 5 × 10 = 50 で 50 の力しかいりませんが、質量 m = 100の時は、F = 5 × 100 = 500 で、なんと10倍もの力が必要ですね!
運動方程式はしっかり使い方を練習してください。いくつかポイントがあります。
1. しっかり力を考える。
F が分からないと運動方程式は解けなくなります。
これは図を描く訓練をしていくうちに身に着くと思います。
2. 斜めの力が混ざっている場合は、sin, cosを使って、縦と横に分ける。
縦は縦、横は横、と運動方程式をそれぞれ分けて考えます。
3. 速度が変わらない時(=等速運動)、加速度 a = 0 になる。
力学的エネルギー保存の法則
力学的エネルギー保存の法則は使いどころをしっかり押さえたい法則です。
さて、正確な話はいったんおいておいて、たとえ話をしましょう。
A君が1000円、B君が0円持っているとします。
二人合わせて1000円ですね。
A君がB君に300円渡すと、A君は700円に、B君は300円に変化します。
しかし、二人合わせた合計額は1000円のままです。
力学的エネルギー保存の法則、と名前は難しそうですが、要は言っていることはこれなのです。
A君のことを運動エネルギー
B君のことを位置エネルギー
二人の合計を力学的エネルギー
と思うと、それがそのまま力学的エネルギー保存の法則を表します。
この法則を使う問題ですが、大体、次のような時はもしかして? と思ってください。
・最高点の高さを求めよ(最高点では v = 0 というのが大事)
・バネが自然の長さになったときの速さを求めよ(自然の長さのとき x = 0)
・ある地点での速さを求めよ
などです。
速さを求めるときは等加速度直線運動の公式を使うかどうか迷うことがあると思いますが、時間 t が関係なさそうなら、大体、力学的エネルギー保存の法則でいけます。
もう少し詳しく見てみましょう。
エネルギー、という言葉は日常でも良く使いますが、なんとなく曖昧な言葉ではないでしょうか。
物理ではエネルギーは、物を動かしたり、変形させたりするのに必要なもの、と考えてください。
燃料がないと車は動かないですし、これはすんなり受け入れやすいと思います。
力学的エネルギーは
力学的エネルギー = 運動エネルギー + 位置エネルギー
というものです。
運動エネルギーの公式は
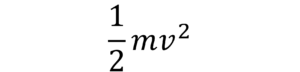
です。
速ければ速いほど、大きなエネルギーを持っている、というのは体感で分かるのではないでしょうか。
ゆっくり進む三輪車と、猛スピードで突っ込んでくるトラック、どちらが危ないかは考えるまでもありません。
しかし、これがなぜ速度の二乗なの?
というのは説明できなくもないですが、覚えた方が早いでしょう。
理屈を考えるのも大切なのですが、人間、
どこかで割り切りも大切
です。
どこをきちんと理解して、どこを暗記していくか、という見極めは数学や物理では重要になるかもしれません。
あまり理由にこだわりすぎるとせっかくの勉強時間を無駄にしてしまいますからね。
位置エネルギーは問題によって変わります。考えている状況によって使い分けてください。
地球の表面近くを考えている時は
![]()
ここで、g は重力加速度(よく9.8m/s^2となっている量ですね)、 x は地面からの高さで、 h と書くことも多いです。
高いところから落とした方が衝撃は強くなる、というのも直感的ですね。
バネにつながれている時は
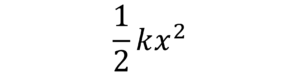
kはバネ定数 [N/m] で伸ばしにくさを表した量です。
x はバネが自然の長さからどれだけ伸びたかを指しています。
※これも説明しませんが、興味のある人はバネを伸ばすのに必要な力と長さのグラフを考えてみるとよいでしょう。
この面積がエネルギーになります。
等加速度直線運動で速さと時間のグラフから公式を出したのと似たようなことができます。
この節の最後に式3を思い出してみます。

上の式ですね。a = -g (重力加速度)として、この式の両辺にm/2をかけるとどうなるでしょうか。
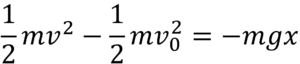
となり、整理すると
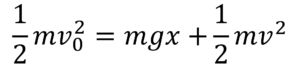
となり、これは最初 v0 で動いていた質量 m の物体が、高さ x 、速さ v に変化した時の力学的エネルギー保存の法則を表しています。
衝突と運動量保存
運動量というのはエネルギーよりもとっつきにくいかもしれません。運動量自体は
運動量 = 質量 m × 速度 v
というシンプルなものです。運動の勢いを表します。これが大きいと勢いがすごいのです。
ですが、なぜ、こんなものを考えないといけないの?
と聞かれると…説明が難しいので、とにかく、考えるといろいろ便利なので、ここも割り切ります。
運動エネルギーとは違うので間違わないようしましょう。
使いどころですが、2つのものがぶつかった、などと問題文にあったら、運動量保存の法則を使います。
もしくは、1つのものが分裂した、という場合もそうなります。
最初にそれぞれあった運動量は衝突によって、変わってしまいますが(速度が変わるので、当然ですね)、それでも二つの運動量を足したものは変わらない、というのが運動量保存の法則の内容です。
この手の法則を使うときは、縦方向と横方向に速度を分解して、縦の運動量保存と横の運動量保存を考えます。
ここでもsin, cosが必要なので、繰り返しますが、この分解は本当によく練習しましょう。
試しに次のような問題を考えます。
最初、横方向に質量10で速さ V の物体が図のように分裂しました。
上の方の分裂後の質量を2, 速度を v1, 下を質量8, 速度 v2 にします。
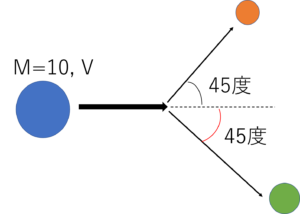
まず、縦方向の運動量保存はどうなるでしょうか(好きな方向から考えてよいです)。
分裂前の状態では横方向の速さしかないので、縦の速さは 0 ですね。
つまり、分裂前の運動量は 0 です。
分裂後では、それが上の方は 2 v1 sin45°、下の方では -8 v2 sin45°になりますよね(下向きに動くのでマイナスの符号がつきます)。
![]()
横方向は同じように考えると
![]()
後はこの連立方程式を解いて v1, v2 を求める、ということになります。
【中学・高校生】通学リュック・カバンおすすめ人気30選!大容量・かわいい・女子男子・選び方も解説!
まとめ
ここまで、お読みいただきありがとうございます。
力学について書きましたが、ここまでの流れを踏まえて他の分野も勉強していけると思います。
大切なことは
・数式の前に言葉の意味をしっかり押さえる
・図をきちんと描く
・公式が出てきたら、実際に問題を解いてみて使い方に慣れる
です。ぜひ、物理を得点源にしてみてください。
この記事の筆者は、旧帝国大学にて物理学の博士号(Ph.D.)を取得した、とぷぶが担当いたしました。学習塾での講師もおこない、物理の苦手な生徒への指導経験も豊富です。物理を数式よりもイメージや言葉で理解することを大切にしており、多くの生徒の成績向上に貢献してきました。
高校生におすすめの問題集は
・英語の問題集おすすめ20選!
・国語のおすすめ問題集
・社会のおすすめ問題集
・化学のおすすめ問題集
も参考にしてください!
スタペンドリルTOP | 全学年から探す
幼児 | 運筆 ・塗り絵 ・ひらがな ・カタカナ ・かず・とけい(算数) ・迷路 ・学習ポスター ・なぞなぞ&クイズ
小学1年生 | 国語 ・算数 ・英語
小学2年生 | 国語 ・算数 ・英語
小学3年生 | 国語 ・算数 ・理科 ・社会 ・英語 ・音楽 ・プログラミング ・毎日計算ドリル
小学4年生 | 国語 ・算数 ・理科 ・社会 ・英語 ・音楽 ・プログラミング ・思考力
小学5年生 | 国語 ・算数 ・理科 ・社会 ・英語 ・音楽 ・プログラミング ・思考力
小学6年生 | 国語 ・算数 ・理科 ・社会 ・英語 ・音楽 ・プログラミング ・思考力
【全学年】Z会グレードアップ問題集(無料コラボ教材)
中学生 | 数学 ・英語 ・漢字 ・社会
2024年無料カレンダー